فصل چهارم
تابع
توابع از امکانات بسیار پرکاربرد و اساسی در هر زبان برنامهنویسی به شمار میآیند که دو کارکرد اصلی و مهم دارند: سهولت حل مسائل پیچیده و بزرگ و امکان استفاده مجدد.
برای طراحی و ساخت هر سیستم بزرگ و پیچیدهای لازم است آن را به اجزای کوچکتر تقسیم نمود و هر یک از آن اجزا را بهصورت مستقل و مجزا تولید نمود و سپس این اجزا را به هم متصل نموده و سیستم کامل را از اتصال اجزای کوچکتر و ارتباط آنها ساخت. در زبانهای مختلف امکانات متفاوتی برای این منظور تعبیهشده است. یکی از سادهترین این امکانات، استفاده از توابع است که تا حدی میتواند این هدف را برآورده سازد. بنابراین یک برنامه بزرگ را میتوان به توابع کوچکتر تقسیم نمود. هر یک از این توابع را بهصورت مستقل برنامهنویسی و تست کرد و سپس با استفاده از این توابع برنامه اصلی را تهیه نمود.
مسائلی که عموماً برنامهنویسان با آنها مواجه میشوند، مسائل جدیدی نبوده و چهبسا پیشازاین برای دیگران نیز پیشآمده باشد و آنها مسئله موردنظر را حل کرده باشند. یکی از اهداف مهم در تولید نرمافزار، استفاده حداکثری از راهکارهایی است که پیشازاین توسط دیگران انجامشده است. به عبارتی سعی میشود حتیالامکان از اختراع دوباره چرخ پرهیز شود. توابع امکان خوبی برای این امر مهیا میکنند. توابع آماده بسیار زیادی قبلاً توسط برنامهنویسان تهیه شده و در اختیار ما است که بهراحتی میتوان از آن استفاده نمود. از طرف دیگر خود ما میتوانیم توابع جدیدی آماده کنیم که هم در پروژههای مختلف خودمان از آن استفاده کنیم و هم امکان استفاده دیگران را نیز از آن توابع فراهم آوریم.
روش طراحی از بالا به پایین
این روش که گاهی آن را روش ساختیافته یا روش تقسیم وظایف نیز میخوانند از رهیافت تقسیم و حمله که در فصل 1 به طور اختصار مطرح کردیم، استفاده میکند.
روش از بالا به پایین روشی برای نوشتن برنامه است که در آن مسئله به زیر¬مسئله¬های سادهتر و قابلفهمتر تقسیم میشود بهطوریکه حل این زیرمسئلهها منجر به حل کل مسئله میشود.
در روش طراحی از بالا به پایین از یک مسئله بزرگ شروع میکنیم و با شکستن آن به زیرمسائل کوچکتر ادامه میدهیم. در هر مرحله زیر مسئلههای بهدستآمده را به مسائل کوچکتر تقسیم میکنیم تا مجموعه زیر¬مسئلههایی را به دست آوریم که قابل شکستن به مسئلههای دیگر نباشند و به اندازه کافی ساده باشند.
با تقسیم مسئله به مسئلههای ریزتر یک ساختاری سلسله مراتبی به نام ساختار درختی ایجاد میکنیم. میزان تجرد هر مرحله از درخت از تجرد مرحله بالاتر کمتر است تا اینکه در آخرین مرحله به مسئلهای برخورد میکنیم که حل آن بدیهی است. به عبارتی مسائل در بالاترین سطح این سلسهمراتب تا حد زیادی انتزاعی و فاقد جزئیات هستند و هرقدر به بخشهای پایینی این درخت نزدیک میشویم جزئیات بیشتری به آن اضافه میشود. شکل 4-1 درختی عمومی یک مسئله نوعی را نشان میدهد. مراحل سایهدار مستقیماً به کد ++C قابل تبدیل هستند، و آنها را مراحل معین (concrete) میخوانیم. مراحلی که سایهدار نیستند را مراحل مجرد (abstract) میخوانیم. هر بلوک نشان داده شده در شکل که ممکن است شامل مراحل مجرد و معین باشد، یک ماژول خوانده میشود.
مرحله معین (Concrete) مرحلهای که جزئیات پیادهسازی دقیقاً مشخص شده است.
مرحله مجرد (Abstract) مرحلهای که جزئیات پیادهسازی هنوز مشخص نشده است.
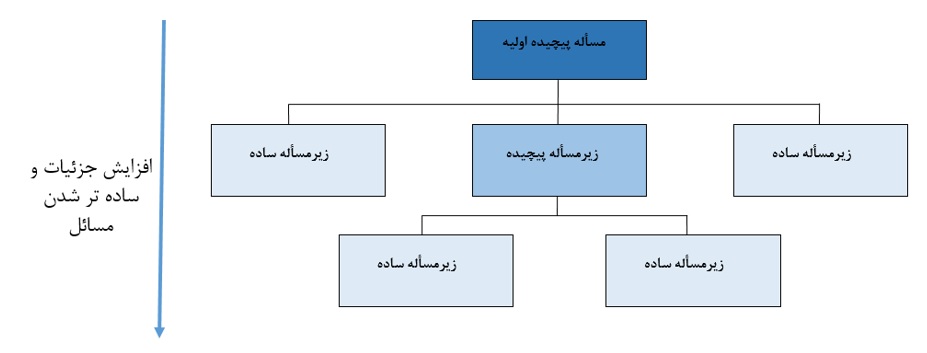
شکل 4-1 : درخت حل مراتبی
به کمک توابع میتوان زیر مسئلههای ساده را در قالب یک تابع پیادهسازی کرد و سپس با ترکیب و تلفیق این توابع به حل مسئله اصلی که پیچیدهتر و بزرگتر است پرداخت. در این فصل با نحوه فراخوانی و تعریف توابع در زبان ++C آشنا خواهیم شد. ابتدا جهت یادآوری از فصل 2، مروری بر توابع ریاضی نظیر توابع مثلثاتی خواهیم داشت.
توابع ریاضی
در ریاضیات توابع بسیاری نظیر سینوس، لگاریتم و قدر مطلق کاربرد دارد. همانگونه که در فصل 2 ذکر شد، این توابع در زبان ++C نیز موجود بوده و قابلاستفاده هستند.
++C دارای یک کتابخانه از توابع ریاضی با سرفصل math.h است که به کمک #include میتواند به کامپایلر معرفی شود. هر کتابخانه در اصل فایلی حاوی مجموعهای از توابع مرتبط به هم است که در کنار هم گردآوری شدهاند. قبل از اینکه از توابع یک کتابخانه استفاده کنیم، باید آن را به سیستم معرفی کنیم. این کار با دستور include انجام میشود:
این دستور به ما اجازه میدهد تا از توابعی که در کتابخانه math معرفی شدهاند استفاده کنیم یا اصطلاحاً آنها را فراخوانی کنیم.
در این مثال تابع ریاضی لگاریتم در پایه 10 فراخوانی شده است. نتیجه اجرای آن این است که لگاریتم 15 محاسبه میشود و در متغیر x قرار میگیرد. در فراخوانی بعدی، مقدار سینوس 1.5 به رادیان را محاسبه میکند. برای محاسبه لگاریتم طبیعی از تابع log استفاده میشود. همچنین برای محاسبه کسینوس و تانژانت از توابع cos و tan استفاده میشود.
دقت داشته باشید که توابع مثلثاتی در ++C ورودی را به رادیان دریافت میکنند. برای تبدیل درجه به رادیان، باید آن را به 360 تقسیم کرد و سپس در دو برابر عدد پی ضرب نمود. عدد پی در کتابخانه مذکور به صورت ثابت M_PI تعریف شده است. بهعنوانمثال محاسبه سینوس 45 درجه به شیوه زیر انجام میشود:
خروجی:
برای محاسبه جذر از تابع sqrt استفاده میشود. اصطلاحاً به هر بار استفاده از یک تابع در فرمولها و محاسبات، فراخوانی تابع گفته میشود. بهعنوانمثال در خط 3 مثال فوق، تابع سینوس فراخوانی شده است.
مثال: برنامهای بنویسید که ریشههای معادله ax^2+bx+c=0 را پیدا کند.
ترکیب توابع
میتوان از یک عبارت ریاضی بهعنوان پارامتر ورودی در فراخوانی یک تابع استفاده نمود. به مثال زیر توجه کنید:
در این مثال ابتدا مقدار عدد پی بر 2 تقسیم میشود سپس با angle جمع میشود و نهایتاً کسینوس آن محاسبه میشود.
در ++C میتوان توابع مختلف را باهم ترکیب کرد. به عبارتی نتیجه یک تابع بهعنوان ورودی تابع دیگر به کار گرفته شود. در مثال زیر ابتدا لگاریتم طبیعی عدد 10 محاسبه میشود و سپس مقدار تابع نمایی آن محاسبه میشود.
مثال: توپی را به هوا پرتاب میکنیم. میخواهیم بدانیم چقدر طول میکشد تا به ارتفاع yc برسد. پاسخ این سؤال را میتوان از رابطه زیر پیدا کرد:
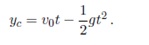
برای حل این مسئله باید آن را بهصورت یک معادله درجه 2 برحسب t بازنویسی نمود:
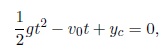
ریشههای این معادله با فرمول زیر قابلمحاسبه خواهد بود:

با توجه به اینکه توپ دو بار یکبار در رفت و دیگری در برگشت به یک ارتفاع میرسد، این معادله دو جواب خواهد داشت. حال این فرمولها را به برنامه تبدیل میکنیم:
تعریف تابع جدید
تاکنون با فراخوانی توابع موجود آشنا شدیم. حال به شیوه تعریف یک تابع جدید در زبان ++C میپردازیم. تابع در زبانهای برنامهنویسی مجموعهای از دستورات است که تحت عنوان یک نام، هدف خاصی را دنبال میکنند و وظیفه مشخصی را به انجام میرسانند. این مجموعه دستورات اصطلاحاً تعریف تابع یا بدنه تابع را مشخص میکنند. تعریف تابع از دو بخش تعریف عنوان و تعریف بدنه تشکیل میشود. در عنوان تابع باید نام آن و لیست پارامترها مشخص شود. قالب تعریف تابع بهصورت زیر است:
…
برای هر تابع یک نام انتخاب میشود. پس از نام تابع لیست پارامترها در بین پرانتز قرار میگیرد. یک تابع میتواند هیچ پارامتری نداشته باشد یا دارای چندین پارامتر باشد. عنوان تابع مشخص میکند که چگونه میتوان از آن تابع استفاده کرد و آن را فراخوانی نمود. در ابتدای تعریف عنوان تابع، باید نوع خروجی تابع نیز مشخص شود. بهعنوانمثال، خروجی تابع سینوس از نوع عدد حقیقی یا double است. همچنین خروجی تابع فاکتوریل عدد صحیح یا int خواهد بود.
پس از تعریف عنوان تابع در خطوط بعدی دستوراتی ذکر میشود که بدنه تابع را تشکیل میدهند و مشخص میکنند که تابع چه کاری انجام میدهد و چگونه وظیفهای را که به عهدهاش گذاشته شده است را به انجام میرساند.
انتخاب نام تابع دلخواه است ولی نباید از کلمات کلیدی زبان ++C که پیشازاین معرفی شد استفاده شود. تمام شرایطی را که پیشازاین برای انتخاب نام متغیرها توضیح دادیم، اینجا هم باید رعایت شود. همچنین تعداد دستورات بدنه تابع دلخواه است. همه این دستورات باید دارای تورفتگی باشند. یعنی سه کاراکتر خالی قبل از آن نوشته شود. چنانچه یک تابع پارامتر نداشته باشد، پرانتز خالی گذاشته میشود. مرسوم است قبل از تعریف هر تابع، یک یا دو خط خالی رد میشود که خوانایی برنامه افزایش یابد، همچنین میتوان یکی دو خط توضیح نیز قبل از شروع تابع نوشت. به تابع زیر توجه کنید که یک خط با علامت = چاپ میکند:
ازآنجاکه این تابع عملاً محاسبات خاصی انجام نمیدهد و مقدار خاصی برنمیگرداند، به جای نوع داده خروجی از void استفاده کردهایم. کلمه void در اینجا به معنی تهی بوده و نشان میدهد که این تابع هیچ مقدار خاصی را باز نمیگرداند.
در نامگذاری توابع تهی به خاطر داشته باشید که این تابع در فراخوانی به چه صورتی ظاهر میشود. عبارت فراخوانی یک دستور است و لذا باید شبیه یک دستور یا دستورالعمل برای کامپیوتر باشد. ازاینرو بهتر است نام توابع تهی از نوع فعل امر باشد.
یک تابع تهی مقدار تابعی را برنمیگرداند. وقتی کنترل به انتهای بدنه تابع میرسد؛ یعنی بعد از اجرای آخرین دستور؛ کنترل از اختیار تابع خارج میشود، و به تابع فرا خواننده بازمیگردد. بهعبارتدیگر صورت دیگری از دستور return وجود دارد که چنین است:
این دستور تنها برای توابع تهی مجاز و معتبر است. این دستور در هر کجای بدنه تابع میتواند ظاهر شود، و سبب میشود که کنترل از تابع فوراً خارج شود و به تابع فرا خواننده بازگردد.
چنانچه تابع از نوع محاسباتی بوده و لازم است مقداری را بهعنوان نتیجه بازگرداند، باید مقدار برگشتی با دستور return مشخص شود. این دستور تعیین میکند که چه مقداری باید بهعنوان نتیجه اجرای تابع برگردانده شود. به مثال زیر دقت کنید:
این تابع که وظیفه محاسبه مساحت دایره را بر عهده دارد، یک پارامتر ورودی برای دریافت شعاع دایره دارد (radius). به نحوه تعریف لیست پارامترها دقت کنید. قبل از هر پارامتر باید نوع داده آن مشخص شود. درصورتیکه تابع بیش از یک پارامتر داشته باشد، با ویرگول از هم جدا میشوند.
پارامترها ابزاری برای ارتباط دو تابع هستند. پارامترها، تابع فرا خواننده را قادر میسازند تا مقادیری را به عنوان ورودی به تابع جهت پردازش منتقل کنند ـ در بعضی موارد ـ تابع فراخوانده شده نتایجی را به فراخواننده باز میگرداند. پارامترها در فراخوانی تابع پارامترهای واقعی (Actual Parameters) خوانده میشوند. پارامترهایی که در عنوان تابع ذکر میشوند پارامترهای صوری (Formal Parameters) خوانده میشوند. (بعضی برنامهنویسان کلمات آرگومان واقعی و آرگومان صوری را به ترتیب بجای کلمات فوق بکار میبرند. بعضی دیگر کلمه آرگومان را بجای پارامتر واقعی و پارامتر را بجای پارامتر صوری بکار میبرند).
پارامتر صوری (Formal Parameters) متغیری که در عنوان تابع اعلان میشود.
پارامتر واقعی (Actual Parameters) متغیر یا عبارتی که در فراخوانی تابع ذکر میشود.
اگر بیش از یک پارامتر به تابع منتقل شود، پارامترهای صوری و واقعی با موقعیت نسبی آنها در دو لیست پارامترها با یکدیگر تطابق داده میشوند.
مساحت محاسبهشده در متغیر s قرار میگیرد و نهایتاً در خط آخر، مقدار این متغیر با دستور return بهعنوان نتیجه تابع برگردانده میشود. علاوه بر اینکه یک متغیر میتواند بهعنوان نتیجه جلوی دستور return قرار گیرد، میتوان از مقدار مشخص و یا یک عبارت نیز مستقیماً استفاده نمود. تابع فوق به شکل زیر هم قابل نوشتن است که در آن عبارت محاسباتی مستقیماً برگردانده میشود.
اگرچه شکل دوم قدری مختصرتر به نظر میرسد، ولی باید توجه داشته که رفع خطا در حالت اول راحتتر است.
یک تابع در حالتهای خاص میتواند بیش از یک دستور return داشته باشد. به مثال زیر توجه کنید:
در این تابع که وظیفه محاسبه قدر مطلق یک عدد را به عهده دارد از دو دستور return استفاده شده است که اولی برای اعداد منفی و دومی برای اعداد مثبت و صفر کاربرد خواهد داشت. نکته قابلتوجه اینکه همیشه در توابع یکی از این دستورات return اجرا خواهد شد و هیچگاه هر دو اجرا نمیشوند. در مثال فوق یک عدد یا مثبت است و یا منفی و هیچگاه هر دو شرط برقرار نخواهد بود. اجرای تابع با اولین دستور return که اجرا شود خاتمه پیدا میکند و دستورات پس از return اجرا نخواهند شد.
توابعی که دارای حاصل هستند یا به عبارتی مقدار خروجی دارند باید بهگونهای طراحی شوند که حتماً در همه شرایط و با همه مقادیر مقدار مناسبی را برگردانند. درصورتیکه برای یک حالت خاص (پارامتر خاص) مقدار بازگشتی تعیین نشده باشد، خطای کامپایل اعلام میشود.
به مثال فوق توجه کنید که در آن برای حالت 0 هیچ مقداری برگردانده نمیشود. در صورت فراخوانی تابع با پارامتر 0 مقدار خروجی برابر NAN یا 0 خواهد بود که نشاندهنده عملکرد اشتباه تابع است، یعنی هیچ مقدار درستی برای آن تعریف نشده است.
روش صحیح نوشتن تابع
در این بخش با استفاده از یک مثال به روش درست نوشتن توابع خواهیم پرداخت. فرض کنید میخواهیم تابعی بنویسیم که فاصله اقلیدسی دو نقطه (x1,y1) و (x2,y2) را محاسبه کند. در ابتدا باید فرمول محاسبه فاصله را پیدا کنیم. برای این منظور میتوان از قضیه فیثاغورث استفاده نمود.
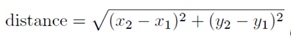
در نوشتن توابع در اولین قدم باید عنوان یا امضای تابع تعریف شود. این تابع باید چهار پارامتر برای دریافت مختصات دو نقطه داشته باشد. تعریف عنوان تابع بهصورت زیر است:
همانگونه که مشاهده میشود، فعلاً بدنه تابع خالی است و صرفاً یک دستور return برای برگرداندن نتیجه در آن قرار دارد. فعلاً فرض میکنیم همواره نتیجه 0 برگردانده شود. درواقع هنوز تا این مرحله هیچ محاسبهای انجام نمیشود. تکمیل بدنه تابع بهصورت تدریجی انجام خواهد شد. اگرچه هنوز این تابع کامل نیست ولی در همین مرحله هم میتوان آن را فراخوانی نمود. طبیعتاً در این مرحله نتیجه 0 محاسبه خواهد شد.
در مرحله بعدی محاسبه فاصله عمودی و افقی را به تابع اضافه میکنیم که این دو مقدار در متغیرهای dx و dy قرار میگیرند. همچنین دستوراتی را جهت نمایش این دو مقدار به تابع اضافه میکنیم.
حال در همین مرحله یکبار دیگر تابع را فراخوانی میکنیم تا از صحت عملکرد آن تا این مرحله مطمئن شویم. به عبارتی بهتدریج که بدنه تابع تکمیل میشود باید آن را تست کرد تا از صحت تغییرات و کدهای نوشتهشده مطمئن شویم. چنانچه تابع با اهمان پارامترهای قبلی فراخوانی شود، انتظار داریم اعداد 3 و 4 را چاپ کند.
در مرحله بعد، محاسبه مجذور فاصله از طریق فرمولی که پیشتر ارائه شد به بدنه تابع اضافه میشود. ازآنجاکه نسبت به محاسبه صحیح dx و dy مطمئن شدهایم، خطوط مربوط به چاپ این دو متغیر را از بدنه تابع حذف خواهیم کرد. اصطلاحاً به این کدها که در فرایند برنامهنویسی نوشته میشوند اما از نسخه نهایی حذف میشوند و کاربرد آنها صرفاً در تست و پیدا کردن خطاهای احتمالی است، داربست گفته میشود.
همانگونه که ملاحظه میشود هنوز مقدار بازگشتی 0 است اما مقدار فاصله توسط تابع چاپ خواهد شد. مجدداً اگر این تابع با همان مقادیر قبلی فراخوانی شود، مقدار 25 چاپ خواهد شد که همان مجذور فاصله است.
در مرحله بعد محاسبه فاصله اضافه میشود. بنابراین باید جذر عبارت محاسباتی قبلی محاسبه گردد. این کار با استفاده از تابع ریاضی sqrt انجام میشود:
در این مرحله که مرحله پایانی است، مقدار نهایی محاسبه شده بهجای 0 برگردانده میشود. اکنون تابع موردنظر کامل شده است.
همانگونه که ملاحظه شد، تکمیل تابع در چند مرحله انجام میشود. تکمیل تدریجی بدنه تابع بسیار مهم بوده و باعث میشود امکان تست و کشف خطاهای احتمالی آسانتر شود و درنتیجه در وقت برنامهنویس صرفهجویی شود. ازآنجاکه در هر مرحله تنها چند خط یا دستور به برنامه اضافه میشود، تست آن بسیار دقیقتر و سادهتر خواهد بود.
مثال: تابعی بنویسید که عدد n را بهعنوان ورودی دریافت و n! را محاسبه و چاپ کند.
ترکیب توابع
این امکان وجود دارد که در بدنه یک تابع، تابع دیگری را فراخوانی کرد. برای روشنتر شدن موضوع به مثال زیر توجه کنید:
مثال: تابعی بنویسید که اعداد m و n را دریافت کند و تعداد جایگشتهای مختلف آنها را چاپ کند.
حل: میدانیم رابطه زیر برای به دست آوردن تعداد جایگشت¬های مختلف n از m وجود دارد:

تابع محاسبه تعداد جایگشت¬ها بهصورت زیر است:
همانگونه که مشاهده می¬شود، در تعریف این تابع از تابع فاکتوریل که کمی قبل¬تر آن را تعریف کردیم استفاده شده است. این مثال نشان می¬دهد که چگونه می¬توان در تعریف یک تابع جدید از توابع قبلی استفاده نمود.
مثال: تابعی بنویسید که مختصات مرکز دایره (xc,yc) و مختصات یک نقطه در محیط آن (xp , yp) را دریافت کند و مساحت آن را محاسبه کند.
برای حل این مثال میتوانیم از توابعی که پیشازاین تعریف کردهایم، استفاده کنیم. شعاع دایره را میتوانیم با استفاده از تابع distance به شکل زیر محاسبه کنیم:
با داشتن شعاع دایره، با استفاده از تابع area که قبلاً تعریف کردیم، میتوانیم مساحت را محاسبه کنیم:
تابع موردنظر را میتوان با ترکیب دو تابع مذکور بهصورت زیر طراحی کرد:
تابع با مقدار خروجی بولین
توابع میتوانند خروجی غیر عددی هم داشته باشند. بهعنوانمثال خروجی یک تابع میتواند بولین باشد. به مثال زیر دقت کنید:
تابع فوق مشخص میکند که آیا x به y بخشپذیر است یا خیر؟ فراخوانی این تابع بهصورت زیر انجام میشود:
خروجی:
از توابع با خروجی بولین میتوان در دستورات شرطی نیز استفاده نمود:
دقت داشته باشید که شرط دستور if در این مثال معادل شرط زیر است و درواقع هیچ تفاوتی ندارد، اما مقایسه نتیجه با True غیرضروری است و رایج نیست:
محل صحیح تعریف تابع
تعاریف توابع C++ به هر ترتیبی میتوانند در برنامه ظاهر شوند. مثلاً میتوانستیم مکان قرار گرفتن تابع main را بجای ابتدا در انتها قرار دهیم، اما اغلب برنامهنویسان C++ تابع main را در ابتدا قرار میدهند و توابع پشتیبان دیگر را بعد از آن قرار میدهند.
درصورتیکه بخواهیم تابع را پس از تابع main یا تابع دیگری که قرار است از آن استفاده کند تعریف کنیم، باید حتماً قالب آن را قبل از آن تعریف کنیم. در غیر این صورت، کامپایلر آن تابع را نخواهد شناخت و خطا خواهد گرفت. در تعریف مذکور نیازی به نوشتن بدنه تابع نیست ولی باید نام، نوع داده خروجی و نوع داده پارامترها مشخص شود. این موضوع در مثال زیر نشان داده شده است.
جریان اجرای برنامه
اجرای برنامه همیشه از اولین دستور برنامه شروع میشود و سپس خط به خط از بالا به پایین ادامه پیدا میکند. هر تابع حتماً باید قبل از اولین جایی که استفاده میشود، تعریف شده باشد. نکته بسیار مهم این است که تعریف تابع به معنای اجرای آن نیست. به مثال زیر توجه کنید:
در این مثال ابتدا تابع printLine تعریف شده است و سپس دستورات برنامه که در اینجا تنها شامل یک دستور چاپ است نوشتهشده است. اجرای برنامه از اولین دستور یعنی دستور زیر آغاز میشود:
در این مثال اصلاً تابع printLine اجرا نخواهد شد، زیرا در برنامه فراخوانی نشده است.
فراخوانی توابع روند اجرای عادی برنامه را تغییر میدهد. به عبارتی وقتی یک تابع فراخوانی میشود، ابتدا تمام دستورات بدنه آن اجرا میشوند و سپس دستور بعدی برنامه ادامه پیدا خواهد کرد. نکته مهم این است که این مسئله را در هنگام خواندن یک برنامه مدنظر قرار دهید. یعنی وقتی میخواهید نحوه اجرای برنامه را درک کنید، یا بهصورت دستی محاسبه کنید که برنامه چه خروجی تولید میکند باید به همین ترتیب عمل کنید.
محدوده پارامترها
همانگونه که ذکر شد، هر تابع میتواند یک یا چند پارامتر ورودی داشته باشد. پارامترها درواقع متغیرهای خاصی هستند که جهت ارجاع مقادیر به یک تابع و کنترل روند اجرایی آن به کار میروند.
پارامترها و متغیرهایی که درون یک تابع تعریف شوند، محلی محسوب میشوند. بهعبارتدیگر خارج از آن تابع قابلاستفاده نیستند و بهمحض اتمام تابع نابود میشوند. به مثال زیر توجه کنید:
در این مثال یک تابع ساده جمع با دو پارامتر تعریف شده است که جمع آن دو را به عنوان نتیجه برمیگرداند. وقتی اجرای تابع تمام میشود، متغیر z و پارامترهای x و y نابود میشوند. بنابراین چنانچه بخواهیم در تابع main از آنها استفاده کنیم (مشابه مثال بالا)، پیغام خطا دریافت خواهیم کرد که x تعریف نشده است:
متغیر محلی (Local Variable) متغیری که داخل یک بلوک اعلان شده و خارج این بلوک قابل دسترسی نیست.
استک اجرای تابع
برای درک بهتر نحوه اجرای تابع و پاس شدن پارامترها به آن و محدوده متغیرها و پارامترها از نموداری به نام نمودار استک استفاده میشود. در این نمودار به ازای هر تابع یک قاب یا مستطیل کشیده میشود. یک قاب هم برای برنامه اصلی رسم میشود. متغیرهای تعریف شده در محدوده هر یک از توابع یا برنامه اصلی در هر یک از قابها نشان داده میشود. همچنین مقادیر هر یک از این متغیرها یا پارامترها در جلوی آن نشان داده میشود. برای روشنتر شدن موضوع به شکل 4-2 توجه کنید. همان¬گونه که در این شکل مشخص است، ابتدا مقادیری به متغیرهای a و b اختصاص داده می¬شود. سپس با فراخوانی تابع، مقادیری که در فراخوانی مشخص شده نظیر به نظیر به پارامترهای مربوطه (x و y) تخصیص پیدا می¬کند. هر یک از متغیرها یا پارامترها در محدوده خود شناخته می¬شوند و خارج از آن قابلشناسایی نیستند. محدوده متغیرها در شکل 4-2 نشان داده شده است.
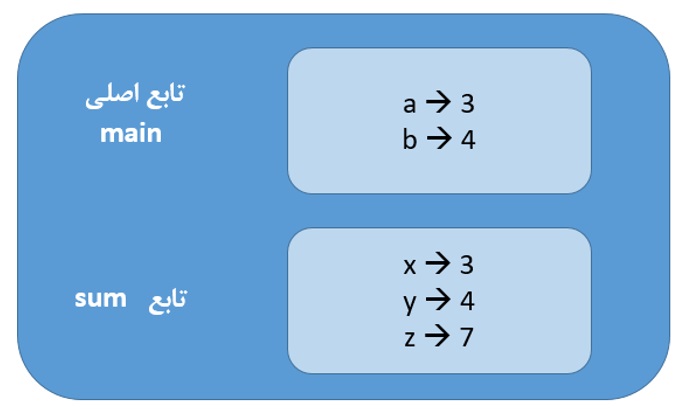
شکل 4-2: نحوه ارسال مقادیر به پارامترها در فراخوانی تابع
تعریف یک کتابخانه جدید
پیشازاین با نحوه استفاده از کتابخانه math آشنا شدیم. در این بخش نحوه تعریف یک کتابخانه جدید از توابع را فرا خواهیم گرفت. یک کتابخانه شامل مجموعه¬ای از توابع مرتبط با هم است که در یک موضوع خاص (نظیر محاسبات ریاضی) تعریف شده و قابلاستفاده است. نحوه تعریف یک کتابخانه جدید را با یک مثال توضیح خواهیم داد.
مثال: فرمول محاسبه ارزش پول در سرمایه¬گذاری بانکی زیر را در نظر بگیرید که در آن A0 مبلغ سرمایهگذاری یا همان پول اولیه، p درصد سود سالانه بانکی و A ارزش پول بعد از گذشت n روز است.
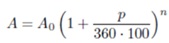
با استفاده از این رابطه میتوانیم هر یک از سه پارامتر دیگر A0، P و n را نیز برحسب سایر پارامترها محاسبه کنیم:
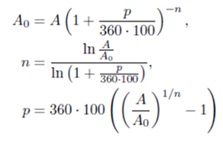
چهار تابع برای محاسبه این چهار فرمول برحسب سه پارامتر دیگر بنویسید.
حل: با توجه به اینکه فرمول محاسبه چهار پارامتر مذکور مشخص است، توابع مربوطه بهصورت زیر تعریف میگردد:
حال این چهار تابع را در یک فایل جدید به نام npv.h ذخیره میکنیم. برای این کار کافی است یک فایل خالی در همان محیط برنامهنویسی خود ایجاد کنید و کد این چهار تابع را در آن کپی نمایید و آنها به نام دلخواه با پسوند .h ذخیره کنید. جهت استفاده از توابع موجود در این کتابخانه جدید کافی است بهصورت زیر عمل کنیم:
بهاینترتیب همه توابعی که در آن تعریف شدهاند در دسترس خواهند بود.
فایلهای سرفصل (Header Files)
از ابتدای کتاب تاکنون بهدفعات از راهنمای #include استفاده کردهایم. این راهنما از پیش پردازنده C++ درخواست میکند تا محتویات فایلهای سرفصل را به برنامه ما اضافه کند.
در این فایلهای سرفصل دقیقاً چه چیزی وجود دارد؟
مطلب پیچیدهای راجع به آنها وجود ندارد. محتویات آنها چیزی غیر از یک سری اعلان C++ نیست. اعلان ثوابت نامداری نظیر INT_MAX، INT_MIN و اعلان متغیرهایی نظیر cin و cout در فایلهای سرفصل فوق انجام میگیرد. اما اکثر محتویات فایلهای سرفصل، اعلان الگوی توابع است.
فرض کنید در عبارتی به تابع کتابخانهای sqrt نیاز داشته باشید. میدانیم هر شناسهای قبل از استفاده باید اعلان شود. اگر گنجاندن فایل سرفصل math.h فراموش شود، کامپایلر پیام خطای "UNDECLARED IDENTIFIER" را صادر خواهد کرد. فایل math.h شامل تابع الگو برای sqrt و دیگر توابع کتابخانهای ریاضیاتی است. با گنجاندن این فایل سرفصل در برنامه، کامپایلر نهتنها شناسه sqrt را خواهد شناخت، بلکه نحوه فراخوانی آنها توسط برنامهنویس به لحاظ تعداد پارامترها و نوع آنها مورد آزمایش قرار میدهد، و در صورت بروز خطا پیام مناسب را خواهد داد.
فایلهای سرفصل دردسر تعیین همه الگوهای توابع کتابخانهای توسط برنامهنویس در ابتدای برنامه را از وی رفع میکنند. با تنها یک خط … #include پیش پردازنده را برای یافتن فایل سرفصل و گنجاندن الگوهای توابع در برنامه بکار میگیریم.
پارامترها
وقتی تابعی اجرا میشود، از پارامترهای واقعی که در حین فراخوانی به آن داده شده است استفاده میکند. چگونه اینکار انجام میشود؟ جواب این سؤال به نوع پارامترهای صوری بستگی دارد. C++ دو نوع پارامتر صوری را پشتیبانی میکند. پارامترهای مقداری و پارامترهای عطفی. تابع با پارامتر مقداری، که بدون علامت & (آمپرسند) ، در انتهای نام نوع داده تعریف میشود، کپی مقدار پارامتر واقعی را دریافت میکند. تابع با پارامتر عطفی، که با اضافه کردن علامت & (آمپرسند)، به انتهای نام نوع داده تعریف میشود، موقعیت (آدرس حافظه) پارامتر واقعی را دریافت میکند. در عنوان تابع ذیل Param1 یک پارامتر عطفی است و Param2 و Param3 پارامترهای مقداری هستند به علامت & بعد از int برای Param1 توجه کنید.
پارامتر مقداری (Value Patameter) پارامتری که کپی محتویات پارامتر واقعی نظیر را دریافت کند.
پارامتر عطفی (Referenc Parameter) پارامتری که موقعیت (آدرس در حافظه) پارامتر واقعی نظیر را دریافت میکند.
اکنون به تشریح تفاوت این دو نوع پارامتر میپردازیم. برای این منظور از مثال زیر استفاده میکنیم. فرض کنید میخواهیم تابعی برای تعویض مقدار دو متغیر بنویسیم. به تابع زیر توجه کنید:
در نگاه اول انتظار میرود تابع swap مقدار دو پارامتر ورودی خود را عوض کند. بنابراین به نظر میرسد باید در اجرای قطعه برنامه فوق، خروجی بهصورت زیر به دست آید:
ولی در عمل خروجی زیر حاصل میشود:
دلیل این امر این است که فراخوانی با مقدار صورت گرفته است. در این حالت یک کپی از مقدار پارامترها ارسال میشود و مقدار متغیرهای اصلی (a و b) دستنخورده باقی میماند. حال این تابع را بهگونهای تغییر میدهیم که به فراخوانی با ارجاع تبدیل شود:
با این تغییر نتیجه موردنظر حاصل میشود:
با فراخوانی با ارجاع، عملاً آدرس دو متغیر a و b به تابع ارسال میشود و هرگونه تغییری در تابع روی متغیرهای مذکور اثر میگذارد.
ازآنجاکه در استفاده از پارامترهای مقداری کپیهای مقادیر واقعی ارسال میشوند، هر چیزی مانند ثابتها، متغیرها، عبارات محاسباتی پیچیده میتوانند بهعنوان پارامتر مقداری مورداستفاده قرار گیرند. برای تابع فاکتوریل که پیشتر مثال زدیم، فراخوانیهای ذیل معتبر و مجازند:
در مورد پارامترهای عطفی، فقط ارسال یک متغیر بهعنوان پارامتر مجاز است. بهعنوانمثال:
مجاز است درحالیکه موارد زیر مجاز نیستند:
مجدداً تأکید میکنیم که تعداد پارامترهای واقعی در فراخوانی تابع و تعداد پارامترهای صوری در عنوان تابع باید یکسان باشند . همچنین نوع داده پارامتر واقعی و پارامتر صوری نظیر آن باید یکسان باشد. در مثال ذیل توجه کنید چگونه هر پارامتر صوری با پارامتر واقعی نظیرش تطابق داده میشود.
عنوان تابع: void ShowMatch (float num1, int num 2, char letter)
فراخوانی تابع: ShowMatch (floatVariable, intVariable, charVariable)
اگر پارامترهای نظیر از یک نوع داده نباشند، تبدیل ضمنی نوع داده به وقوع میپیوندد. مثلاً اگر پارامتر صوری از نوع صحیح باشد، و پارامتر واقعی از نوع اعشاری باشد، پارامتر واقعی قبل از ارسال به تابع بهصورت صحیح در آورده میشود. همچنان که در C++ مرسوم است برای جلوگیری از تداخل ناخواسته انواع داده از تبدیل صریح انواع میتوان استفاده کرد.
همچنان که تأکید کردهایم، پارامتر مقداری یک کپی از پارامتر واقعی را دریافت میکند، لذا پارامتر واقعی بهطور مستقیم در دسترس نیست و نمیتوان از طریق کپی آنها تغییر داد. وقتی اجرای تابع تمام میشود، محتویات همه پارامترهای مقداری به همراه متغیرهای محلی از حافظه پاک میشوند. اختلاف بین متغیرهای محلی و پارامترهای مقداری در این است که متغیرهای محلی در ابتدای اجرای تابع تعریف نشده میباشند، حالآنکه پارامترهای مقداری بهطور خودکار با مقادیر نظیر پارامترهای واقعی مقداردهی اولیه شدهاند.
پارامتر عطفی با & بعد از نام نوع داده اعلان میشود. به این اعلان پارامتر، عطفی گفته میشود، زیرا تابع فراخوانی شده میتواند به پارامتر واقعی نظیر، بهطور مستقیم دسترسی داشته باشد. بخصوص تابع مجاز است که در مقدار پارامتر واقعی تابع فرا خواننده دخل و تصرف کرده مقدار آنها تغییر دهد.
وقتی تابعی با استفاده از پارامتر عطفی فراخوانی میشود، موقعیت (آدرس در حافظه) پارامتر واقعی و نه مقدار پارامتر به تابع ارسال میشود. در اینجا تنها یک کپی از داده وجود دارد و توسط تابع فراخوانی شده و تابع فراخواننده مورد استفاده قرار میگیرد. وقتی تابعی فراخوانی میشود، پارامتر واقعی و پارامتر صوری نام¬های مترادفی برای یک موقعیت از حافظه خواهند بود. هر مقداری که تابع فراخوانی شده در این موقعیت قرار دهد همان مقداری است که تابع فراخواننده در آنجا خواهد یافت. بنابراین در استفاده از پارامتر عطفی باید هشیار بود زیرا هر تغییر آن مقدار پارامتر واقعی را تحت تأثیر قرار میدهد. در جدول ذیل انواع پارامترهایی را که تاکنون بررسی کردهایم بهطور خلاصه ذکر شدهاند.
پارامتر مورداستفاده
پارامتر واقعی در فراخوانی تابع ظاهر میشود. پارامتر صوری نظیر آن میتواند پارامتر مقداری یا مرجعی باشد.
پارامتر مقداری صوری در عنوان تابع ظاهر میشود. کپی از مقدار ذخیرهشده در پارامتر واقعی نظیر را دریافت میکند.
پارامتر عطفی صوری در عنوان تابع ظاهر میشود. آدرس یا موقعیت پارامتر واقعی را دریافت میکند.